Week 6: Keys Upon Keys
Hello everyone!
This week I spent my time researching the Elgamal encryption algorithm and learning more about Galois fields, which are relevant to AES. This week was particularly exciting for me, as Elgamal encryption is the last major form of encryption I am planning to research. This means that the next four weeks I will mostly be working on solidifying my knowledge of the encryption algorithms I have already researched, as well as developing activities and hunting for fun facts to include in my pamphlet! The first section of my project was centered around learning the mathematics of encryption; the second section is going to be my attempt at learning to relay this material in a digestible manner. I’m especially excited to be working with Dr. Ismert on this part of the project, as she has lots of experience teaching complex topics to undergraduates who aren’t that different from you or me.
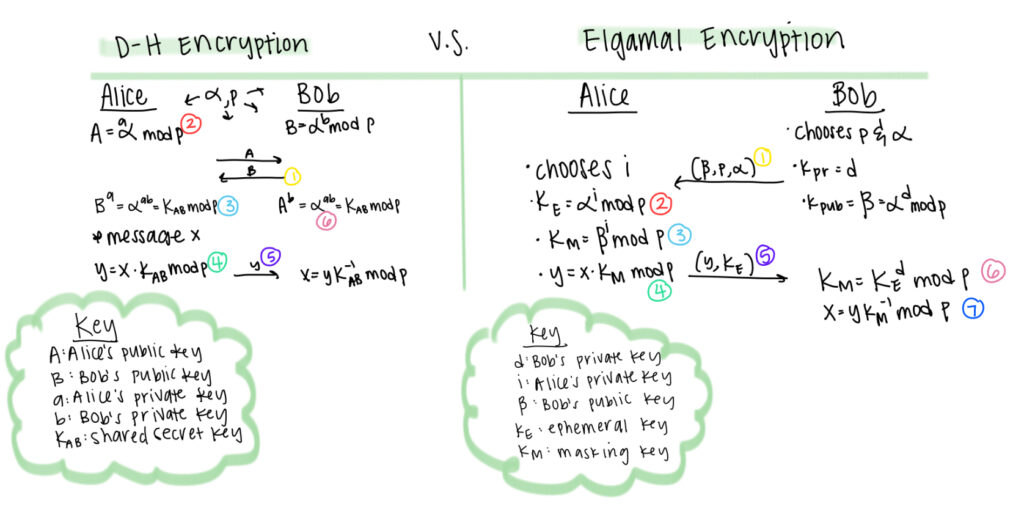
Now, to discuss my research from this week. Elgamal (also written ElGamal) is very similar to Diffie-Hellman (D-H). However, as I distinguished last week, D-H is a key exchange, meaning that it results in a shared private key between two parties. The D-H process alone is not an encryption algorithm. However, with the addition of an extra step, D-H could technically encode messages. Essentially, the private key created by the D-H algorithm could be multiplied with a message consisting of a string of bits to essentially modify the string of bits and create a new ciphertext. Elgamal is essentially this same process with reordered steps that allow for increased security.
I know you are probably sick of reading the words “Diffie-Hellman” so many times over the past three weeks, but I promise that it really is relevant to understanding Elgamal encryption. Rather than rehashing exactly how D-H works, I will outline the most important aspects of the algorithm in comparison to Elgamal’s encryption scheme. In D-H, the two parameters, alpha (the primitive element) and the modulus “p,” are public knowledge and are agreed upon by Alice and Bob. Alice and Bob then each choose private keys “a” and “b,” respectively. These private keys become exponents of alpha to create two separate public keys, which Alice and Bob then exchange. Using each other’s public keys and their respective private keys as exponents once again, Alice and Bob are able to arrive at a shared private key. In order to encrypt a message using this private key, Alice would multiply the message “x” by the shared private key and then send the resulting ciphertext to Bob. Bob would essentially “solve for x” by “dividing” the ciphertext by the private key. In actuality, Bob would multiply the ciphertext by the inverse of the private key, which essentially acts as this “division” process.
In the case of Elgamal, rather than alpha and “p” being chosen by Alice and Bob together, Bob chooses these two elements himself. At the same time, Bob chooses his private key “d” and creates his public key, just as before in D-H, by raising alpha to the “d” power, modulus p. He then sends his public key, alpha, and “p” to Alice. Alice chooses her own private key “i” and creates an “ephemeral key” by raising alpha to her private key, modulus p. I will explain why this aspect of Elgamal is called the “ephemeral key” later on. Alice also calculates the “masking key” by taking Bob’s public key and raising it to her private key modulus p. The masking key is the element that is multiplied by the message “x” to create the ciphertext “y.” Alice then sends the ciphertext to Bob along with the ephemeral key. Bob calculates the masking key by raising the ephemeral key to his private key, mod p. He can then decrypt the ciphertext by multiplying it by the inverse of the masking key, just as in D-H encryption. The images below show the corresponding steps between D-H encryption and Elgamal, as well as a proof of correctness for anyone who wants to know why this process works.
Now to talk a little bit more about why Elgamal is advantageous over D-H encryption. Essentially, each time Bob receives a new ciphertext from Alice, he doesn’t need to create a new public key, whereas D-H encryption would have to be completely redone each time. The only thing that must be altered in Elgamal encryption is Alice’s private key “i.” By changing “i,” the ephemeral key is changed as well, which is exactly why it is called “ephemeral” or “lasting for a short time.” This in turn changes the masking key and ensures that the ciphertext created is new each time Elgamal occurs. Why does this matter? Well, here is a concrete example. Let’s say that Bob is actually Amazon.com and you are Alice, purchasing something online. Let’s say that your message is actually your credit card number. Each time you put in your credit card number, your computer automatically generates a new “i,” ensuring that your credit card is encoded in a new ciphertext each time you make a purchase. Otherwise, Elgamal would be a much less secure process. For these reasons, “D-H encryption” isn’t actually used in the real world. It’s simply a way to relate Elgamal to an aforementioned topic.
In fact, if there was damage to your computer or to the computer chip responsible for randomly generating a new “i,” this would jeopardize the Elgamal encryption scheme. One of the attacks against Elgamal is to purposefully cause physical damage, such as overheating a device, to cause this exact problem. The attacker would know if they were successful because the ephemeral key would never change. Thus, if the attacker had knowledge of any one plaintext, they could decode any other messages encoded on your device. That’s pretty scary! Fortunately, an attacker would have to have access to your device in order to complete this attack. Otherwise, he would be stuck attempting to solve the discrete logarithm problem, a difficult process that I described in my week 4 blog.
Besides studying Elgamal encryption, I also dove down a bit of a rabbit hole this week and learned more about Galois fields, specifically those with polynomial representations. Essentially, in AES, bits are represented by polynomials rather than simple integers. AES itself exists in the Galois field GF(2^8), which essentially means that the coefficients of these polynomials exist in a field modulo 2, and the “Xs” exist in a field modulo a polynomial of degree eight, which acts as a prime number. These polynomials are called irreducible polynomials, meaning that they are not factorable, essentially in the same way that prime numbers only have one and themselves as factors. AES uses the irreducible polynomial X^8+X^4+X^3+X+1. Take, for example, the byte 0000 0100. This byte would be represented by the polynomial “x^2.” The byte 0010 1101 would be represented by the polynomial x^5+X^3+X^2+1. These polynomials will only ever have coefficients of zero or one due to the modulus 2, and they will never have an order greater than 7 because the irreducible polynomial is of order 8. Essentially, it’s the same idea that any number 2 or greater modulo 2 will result in zero or one due to the looping effect. 3 modulo 2 is 1 (3 divided by 2 has remainder 1), 2 modulo 2 is 0, 5 modulo 2 is 1, and so forth. These fields had eluded my understanding until I met with Dr. Ismert this week, so I thought I would shed some more light on them and the inner workings of how bits are truly represented in AES.
That’s all for this week! I can’t wait to see what other interesting things come up as I spend the coming weeks filling in my understanding of the many encryption processes I have studied and beginning the development of my pamphlet!
Comments:
All viewpoints are welcome but profane, threatening, disrespectful, or harassing comments will not be tolerated and are subject to moderation up to, and including, full deletion.