Week 5: New DEScoveries
Hello everyone!
I’m officially halfway through my project and approaching the end of the heavy research section of my project. This week, I dove into the Data Encryption Standard (DES) and revisited RSA to study it more formally. I will start off this post with a discussion of DES, but before I delve into the mathematical process in detail, I want to provide some historical background as to why the creation of DES was a pivotal moment in the history of cryptography. DES was proposed in 1974 by IBM, and up until that point, cryptography was a field limited to intelligence agencies. There simply wasn’t much cryptography in the public space. Upon the request of the U.S. government for an encryption standard, IBM created this cipher, which became available to the entire public. Although the process behind DES remained a secret, this was the first instance in history where the public had access to a secure crypto-system and therefore, greater control over their privacy, rather than having all cryptography used solely by the government. Thus, this encryption code became incredibly widely used, especially in banking.
Today, DES has been replaced by AES, as I mentioned in last week’s post. When DES was first proposed, computers were much slower than they are today, and DES’ algorithm was complicated enough that breaking it by brute force took a long time. However, by the 1990s, computers were much more sophisticated and could successfully break DES in a timely manner. In fact, by 1998, DES could be broken in only 39 days! At this point, there arose a need for a more complicated algorithm, and in response to this need, the National Institute of Standards and Technology (NIST) created a competition to find a more secure encryption standard. In 2001, AES was declared the winner of this competition and became the new standard of encryption that is still widely used today.
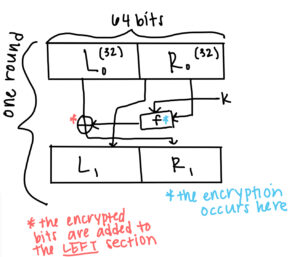
Although DES is essentially an obsolete form of encryption when compared with AES, I still think that it is valuable to look at its process in comparison to the complexity of AES and the ways in which cryptography has developed immensely over the last fifty years. While AES has four multi-layer steps to its process, DES has essentially two main cryptographic operations. DES encrypts plaintext in groups of 64 bits using a 56-bit long key. The plaintext (the string of bits that Alice wants to encrypt) is split into two sections, each of 32 bits. During each round of encryption, only the left 32 bits are encrypted, with the left and right sections swapping spots at the end of each round to ensure that all of the plaintext is encrypted. In total, 16 rounds of encryption occur in DES.
What exactly happens to the left 32 bits during each round of encryption? Initially, a straightforward bit permutation occurs, meaning that the order of all of the 64 bits is changed. Technically, this doesn’t affect the cryptographic process of DES in any way, as the permutation is reversed at the end of each round. The alteration of the order of bits is used only for the more physical process of uploading plain text to computer chips.
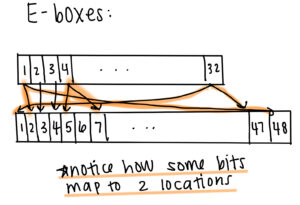
The first true step of the process occurs within E-boxes, which essentially extends the length of the right bit string from 32 bits to 48 bits. This occurs through another permutation, except 16 of the original 32 bits are mapped to two spots, meaning that if one of these bits had experienced a bit flip, two bits in the chain of 48 would now have flipped bits, thereby “diffusing” bit flips along the string. This new bit string is then added to a section of the 56- bit key mod 2 (the mod 2 essentially ensures that the new string is only made of zeros and ones).
The second step of DES is made up of S-boxes, similar to those used in AES. These S-boxes are the heart of DES and provide confusion by causing bit flips throughout the bit string. It is important to note that each of the 8 S-boxes takes in 6 bits but outputs only 4 bits each, ensuring that by the end of the DES encryption process, a bit string of 32 is encoded to become a different string of 32 bits rather than keeping an extra 16 bits from the extension step. Within these S-boxes, the four innermost bits are collected to determine the column of the S-box, and the two outermost bits are collected to determine the row of the S-box. Within the S-box, the row and column dictate a singular number, which is then written in binary form as a string of four new bits. This final string of 32 bits is added to the original left string of 32 bits mod 2, encrypting the left section of bits.
As I mentioned before, at this point, the permutation that occurred before the E-boxes would now be reversed, and the output of this round of encryption would swap places with the right section of 32 bits. The process would then repeat with this new section of plaintext.
As you can see, a critical problem with DES is that it inherently requires a predetermined key length of 56 bits, which is no longer long enough to defend against brute force attacks. Triple DES, an algorithm that completes DES three times with three separate keys, is considered more secure and in some ways, combats this pitfall of DES. However, this process requires triple the computing time to encode text, making AES a more efficient and secure process.
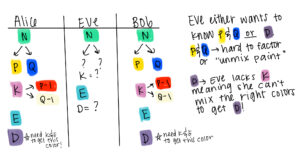
I also want to briefly discuss RSA in more detail. In my first post, I created a visual with different colored “paint” to explain the process. Since then, I have learned a lot more about RSA and encryption in general, and I have realized that my original image does not accurately describe the process of RSA. The picture actually describes a Diffie-Hellman key exchange, which I discussed in detail in my last post. The critical difference between RSA and Diffie-Hellman is that Diffie-Hellman is a key exchange, meaning its purpose is to securely allow Alice and Bob to share a key amongst themselves, which can later be used in an encryption process such as DES or AES. RSA, on the other hand, is an asymmetric encryption algorithm, meaning that it uses one key to encode data and a different one to decode data.
In the case of RSA, a public key N is the product of two prime numbers: “P” and “Q.” The private key that is used for encryption is the product of (P-1) and (Q-1). Another number, “e,” is chosen to be relatively prime to the private key (K). Relatively prime simply means that “K” and “e” don’t share any factors except for the number 1. All of these numbers are then plugged into the encryption equation: X^e mod N, where “X” is the message. In order to decrypt this message, one must complete the equation X^ed mod N, where “d” is the secret decryption key. “d” is a number that is the multiplicative inverse of “e mod K,” meaning that when “e” and “d” are multiplied together and the product is divided by “K,” the remainder is 1. Essentially, in order to find “d,” one must also know “K,” which is a secret key. The premise behind Alice and Bob having knowledge that Eve lacks, which further allows them to decrypt a message, is essentially the same premise as Diffie-Hellman allowing Alice and Bob to arrive at a shared secret key using knowledge Eve cannot access.
The similarities and differences between Diffie-Hellman and RSA are somewhat difficult to understand without a picture, so I have included a comparison of two “paint examples” below, using my original image from week 1 to represent the Diffie-Hellman Key Exchange.
That’s all for this week! In the coming weeks, I plan to fill in a few gaps along the “encryption timeline” and begin working on my pamphlet. In the near future, I promise my posts won’t be nearly as long-winded as the past couple have been. Thank you for sticking with me throughout this process! 🙂
Comments:
All viewpoints are welcome but profane, threatening, disrespectful, or harassing comments will not be tolerated and are subject to moderation up to, and including, full deletion.