Week 3: Again and Again and Again
Hello everybody! This week I explored some more great resources on elliptic curve encryption (ECC) and got a better handle on how exactly data can be encrypted using these funky graphs. One of these resources is actually a series of lectures by Professor Christof Paar, a German mathematician who teaches in, well, Germany. It turns out his lectures are *almost* entirely in English, and who knows, maybe I’ll also pick up on some of the scattered German phrases by the end of this project. On another note, his lectures are incredibly clear and have helped me grasp many of the terms I had previously been struggling to understand from articles and textbooks alone.
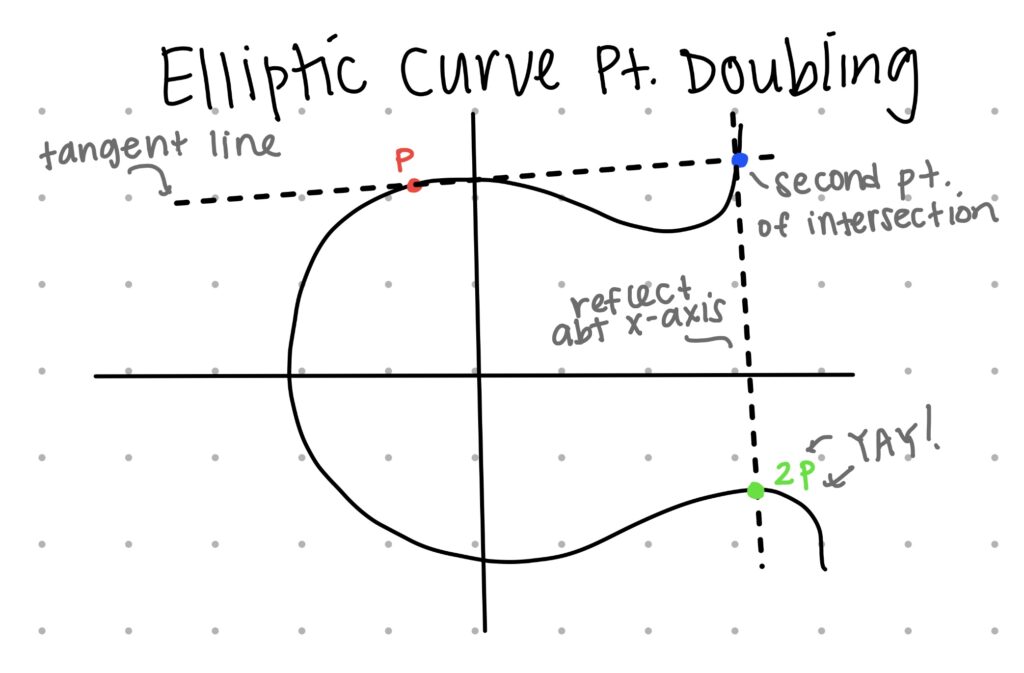
One of the most important terms I learned this week is “cyclic group.” Cyclic groups are necessary in order for ECC to be hard to decrypt, but in order for me to define a cyclic group, I must first define a group. Fundamentally, a group needs both a set of elements (which in this case is the points on the elliptic curve) and an operation (in this case, addition). Last week, I mentioned that the encryption process is based on adding points together to get new ones on the curve. I’ll start off this post by briefly explaining a little bit more about how addition actually works on elliptic curves. From a geometric point of view, when you add two points (P and Q) together, a secant line is drawn through the corresponding points. The third, new, point at which the secant line crosses the elliptic curve is then reflected across the x-axis to give the final point (P + Q). When “doubling” points, or adding P + P to get 2P, the same process is completed, except a tangent line is drawn through point P, and then the second point at which the line crosses the elliptic curve is reflected across the x-axis. That is all wildly confusing when written down, so I’ve drawn a diagram below that shows these processes more clearly.
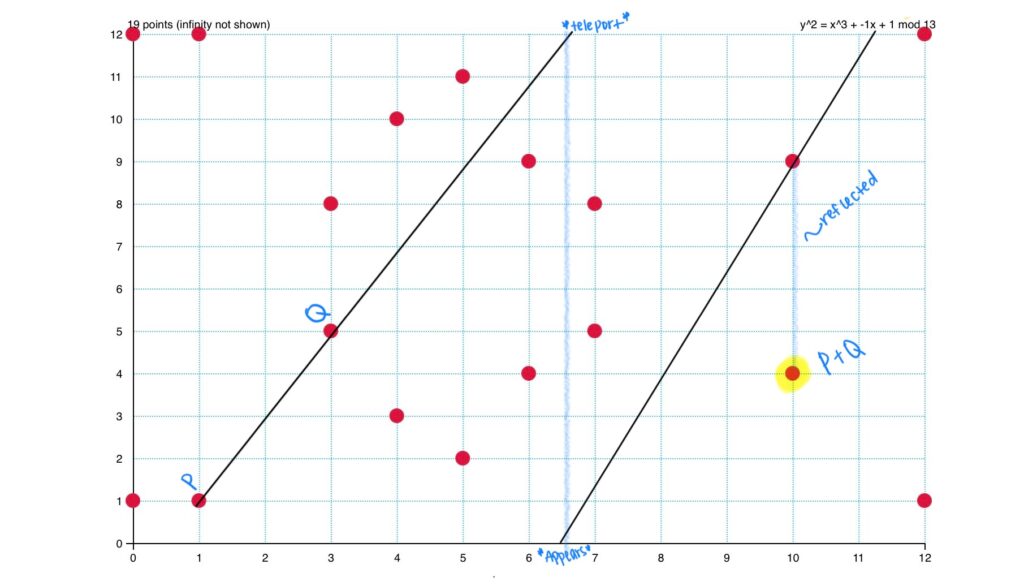
One of the reasons that ECC is so important is its efficiency, as I have mentioned before. Thus, ECC is very common in the technology we use day-to-day, such as when we send messages on our phones. While point addition is necessary for ECC to occur, our phones do not use geometry when adding points. Rather, they use algebraic formulas based on the equations of secant lines and the two points being added, similar to finding the intersection of two linear equations. These formulas are not pretty, however, which is why I chose to explain the additive process geometrically. Additionally, you may remember that the arithmetic of ECC is done modularly, as seen in the odd dot graphs from last week’s post. So, how exactly does adding points work when there isn’t a physical elliptic curve for a line to intersect? Interestingly, it works similarly to the game Asteroids, in which the line connecting two points simply continues bouncing from top to bottom of the graph until it intersects one of the modular points. In other words, like in Asteroids, when the line reaches the top of the “screen,” or in this case the top limit of the modular set, it teleports to the bottom of the “screen,” or the bottom limit of the modular set, and continues on until intersecting a point, which is then reflected across the x-axis as before (elliptic curves are still symmetrical even modularly).
Now, back to defining a “cyclic group.” In order for a group to fall under the “cyclic” category, there must be a primitive element. This primitive element is important in that it can generate all of the other elements within a group. For ECC, the primitive element is the point P, which, when added to itself again and again and again, eventually creates all of the other points on the elliptic curve until it generates itself and the process repeats…again and again and again. That’s pretty wild! Under certain conditions, the points of an elliptic curve form a cyclic group, meaning that all points are some multiple of a generator point P. This idea is the basis of how ECC works.
Think of it this way: if I pick the point T on an elliptic curve, it is part of the cyclic group and thus was generated by the primitive element P. This means that T is a multiple of P, but which exact multiple of P is unknown. For example, T could be 3P, 7P, or 32P; the number of times P was added to itself to get to the point T is unknown. This number is the private key for ECC, and the primitive element itself is the public key. ECC works very similarly to RSA in terms of the encryption process; this time, when modeling the process, however, I am using points rather than colors.
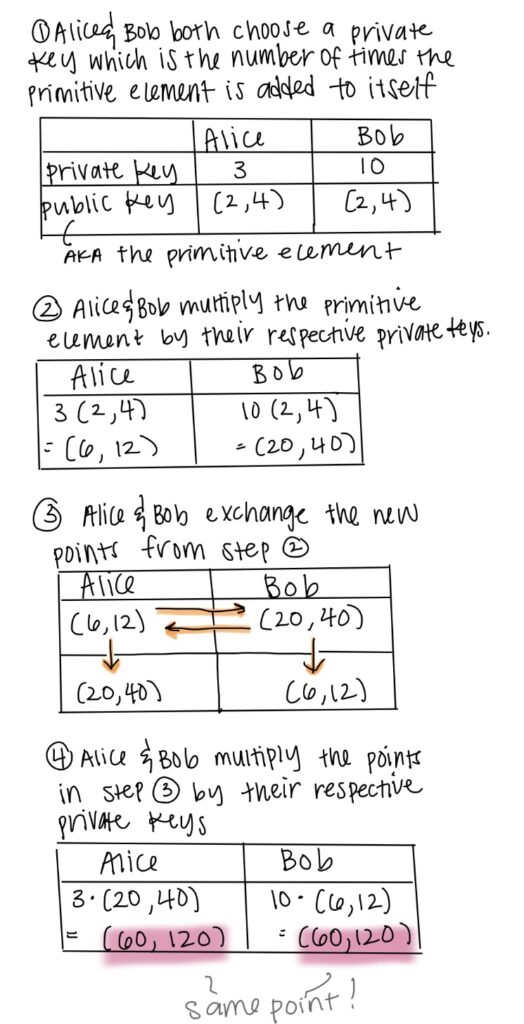
This unique property of some elliptic curves, in which all points form a cyclic group, makes it difficult for cryptographers to randomly choose their own curves that have a primitive element and therefore are viable for ECC to occur. To address this problem, the National Institute of Standards and Technology (NIST) created a list of standard elliptic curves and their primitive points for the use of the public. Because primitive elements alone are not enough to decrypt ECC, Bob and Alice can still choose their private keys, which determine how many times the primitive element is added to itself to arrive at a brand new point. The number of “hops” the primitive element makes can still be a secret, and therefore, the NIST elliptic curves are very convenient as they are already known to meet the criteria of a cyclic group.
Other than researching elliptic curves this week, I also learned a fun fact from my mentor: Wikipedia is actually a very reliable resource in the math field. After so many years of avoiding Wikipedia for any sort of research, it feels wrong to intentionally search for pages on the cryptography I am researching. Next week, I hope to continue watching Professor Paar’s lectures, look into the early beginnings of cryptography (thank you for the idea, Mr. Smith!), and brainstorm activities to put in the interactive pamphlet I plan to include in my final project. I hope you enjoyed this week’s post! Until next time.
Comments:
All viewpoints are welcome but profane, threatening, disrespectful, or harassing comments will not be tolerated and are subject to moderation up to, and including, full deletion.