Week 2: There’s Always More Trap Doors
Hello and welcome back! This week, I spent most of my time searching for and trying out new resources. As I mentioned in my last post, one of the initial struggles I am facing is the process of building up some of the mathematical background information that I lack. After scouring the internet for online courses, I enrolled in a fundamentals of quantum computing course and found a great series of lectures on linear algebra through MIT’s OpenCourseWare website. I hope that by following along with these courses while working on my project, I will be more familiar with some of the notations and computations that arise in my own research.
Aside from finding new resources, I have continued to study RSA encryption and have begun delving into elliptic curve cryptography (ECC) with Dr. Ismert. Both ECC and RSA are similar in that they are trap-door algorithms, public key algorithms, and rely heavily on modular arithmetic. That was a lot of fancy jargon I threw at you, so let me explain each of these similarities a little further. First off, a trap-door algorithm means that cryptography works by utilizing a simple computation to encrypt data and a difficult computation to decrypt data. Last week, I briefly discussed that RSA uses multiplication (an easy process) to encrypt data, but the prime factorization of huge numbers (a hard process) to decrypt data. Similarly, ECC encrypts data by adding points together on a curve to get to a new point (an easy process) and then determining how one arrived at a final point (a hard process). This article describes ECC as a game of billiards. It is an easy process for someone to hit a ball over and over and watch as it moves from point to point. It is very hard for someone who just walked into the room and saw where the ball currently is to decipher how many hits it took to get the ball into that exact place.
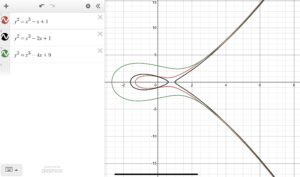
Now, a new term! ECC and RSA are also both public key algorithms, meaning that there are two keys necessary to decrypt the data, one of which is accessible to the general public. This is the key that “Eve” has access to that, along with “Bob” and “Alice’s” private keys, and is critical to the decryption process, but without the private keys, it doesn’t give enough information to an outsider to decrypt the data. Finally, what is modular arithmetic? In both RSA and ECC, calculations are done over a finite set of numbers which “wrap around” after reaching the largest value in the set. Think of it as the remainders when doing division. If the largest number in my set is four, my set of numbers is made up of 0, 1, 2, 3, 4, which in total is a collection of five numbers. Let’s try to get the number 6 in the set. 6 divided by 5 has a remainder of 1, so in this set, 6 would be represented by a 1. Similarly, 5 divided by 5 has remainder 0, so it is represented by a 0. 7 divided by 5 has remainder 2, 8 divided by 5 has remainder 3, and so forth. Another way to think about it is in terms of clocks! Rather than counting every hour of every day, we “reset” at twelve. The thirteenth hour is one o’clock (13 divided by 12 has remainder 1) and the twentieth hour is eight o’clock! In both RSA and ECC, modular arithmetic, specifically with a prime modulus, makes the trap-door function even harder to decrypt, and therefore makes both of these forms of cryptography more secure. Modular arithmetic also ensures that arithmetic is being done over a finite field which generally makes operations “nicer.”
Needless to say, there are many similarities between RSA and ECC, another of which is that neither of them are quantum safe. The most notable difference between the two, however, is that ECC’s trap-door function is much harder to solve than RSA’s. ECC is also more computationally efficient in that it requires much less computing power to create the same level of security as the equivalent form of RSA encryption. A fun fact from the same article I linked above is that in order to break a 228-bit RSA key (a string of 228 zeros and ones) it would take less energy than boiling a teaspoon of water. In order to break an equivalent 228-bit ECC key, it would require the amount of energy it would take to boil all of the water on the planet. That’s a pretty big difference!
That completes the summary of my week two. Thank you for reading!
