The Hohmann Transfer!
Payton M -
Welcome back to my blog!
This week I worked on finding new ways to reduce the amount of fuel used in the code I wrote before T3. I originally used the Hohmann Transfer to get from Earth to Jupiter, however the fuel values were rather large, so I added a section in the code using a Hohmann Transfer to Mars instead to see how the fuel consumption values differed. As anticipated, going to Mars instead of Jupiter used significantly less fuel since it is much closer to Earth and less massive than Jupiter. I can’t wait to see if this option turns out to be more efficient overall after completing the other sections, as the closer the planet is to the sun, the more fuel it takes to go far out and reach Eris.
To construct a mental image of what’s going on, I’ll explain what a Hohmann transfer is and which kind I am using in more detail. A Hohmann transfer is known to be the most fuel-efficient orbit changing maneuver because it only requires a change in velocity and not a change in direction. The image below shows a Hohmann transfer focused around one planet, used to change the orbit altitude of a satellite, for example.
For my project however, I am using an interplanetary Hohmann transfer (HT), which uses the same basic principles of the original Hohmann transfer, but requires a change in the focus (center of an ellipse) of each orbit. The starting point for the HT is the final orbit of the orbit raising maneuvers (ORM) around Earth, with our focus being Earth. The next step is to determine the speed the spacecraft needs to be at location D in its heliocentric (sun-centered) transfer orbit, making the focus the Sun. The first burn of the HT gets the spacecraft from that speed of the final ORM to this speed needed for the HT at point D, notated as VD in the image below. This speed VD accounts for the speed needed to escape Earth’s gravity well. So, after the first thrust burn, the spacecraft will be sent on the Jovian Transfer Trajectory path. Once it reaches Planet 2, it will be traveling slower since it is at its apoapsis location, furthest away from the focus. I am calling this speed the arrival velocity, VA.
*The planets’ velocities (V1 and V2) are used in the equations to determine velocities at locations A and D but are subtracted to find solely the spacecraft’s speed, VD and VA).
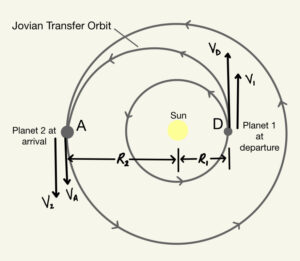
| Variable | Meaning |
| Planet 1 | Earth |
| Planet 2 | Jupiter |
| V1 | Velocity of Planet 1 [km/s] |
| V2 | Velocity of Planet 2 [km/s] |
| R1 | Distance between Sun and Planet 1 [km] |
| R2 | Distance between Sun and Planet 2 [km] |
| VD | Velocity needed for departure [km/s] |
| VA | Velocity at Arrival Location [km/s] |
To analyze more options, I have three sections in the HT stage of the code: 1. Perihelion HT, 2. Aphelion HT and 3. Martian HT. The planets in our solar system in fact have slightly elliptical orbits and are not perfectly circular, giving them each their own perihelion (closest to the sun) and aphelion (furthest from the sun) locations. Option 1 replaces R1 with Rp_E (Earth’s perihelion distance) and R2 with Rp_J (Jupiter’s perihelion distance). Option 2 does the same thing but with the aphelion distance values. Finally, option 3 (the one I added this week) uses the perihelion distances of Earth and Mars.
Thanks for reading this week’s blog, and I can’t wait to share more next week!
Comments:
All viewpoints are welcome but profane, threatening, disrespectful, or harassing comments will not be tolerated and are subject to moderation up to, and including, full deletion.