#9 – Using Pseudoconics to Analyze Non-Euclidean Geometries
Paul N -
Hi, and welcome to week 9 of my Senior Project! This week was cut short by a visit to Michigan, but I still got a lot more done than I expected to. The first thing that I did was that I worked on creating a graph to visualize the transformation between a Euclidean and Non-Euclidean curve for a specific curve and Non-Euclidean geometry. Recall from the previous blog post that to find the Non-Euclidean geometry where the transformation of f(x) onto said geometry is some g(x), all we have to do is set u*(f(x)/x) equal to g(u), so that the curve resulting from the transformation will be (u, g(u)). Let’s take the line y = f(x) = 1, and let’s say that u is the following function of x:
This may seem like an arbitrary and overcomplicated function, but it turns out that, when we recall the following equation from my previous blog post, F(u) simply becomes the square root of u cubed:

This is good because, if you also recall, F(u) is also the integral of the square root of P with respect to u, which can then be used to find the z-component of our Non-Euclidean surface (u, v, z(u,v)). Finding the z-component of the surface is trivial from here, but what we really want in order to visualize the transformation of the Euclidean line y = 1 into this Non-Euclidean curve is an arbitrary variable where, as the variable approaches one value or another, we achieve either our Euclidean line or our Non-Euclidean curve. Thus, let’s define our z(u,v) to be the following:

Now, we have a variable α where, as α approaches infinity, the z-component approaches 0, thus defining a Euclidean plane, and as α approaches 1, we return to our original Non-Euclidean surface. Notice that I also listed Pα and Fα in terms of u (note that Fα(u) and F(u) are not equal, but F(u) is still the square root of u cubed), and this is because now we can recall our equation from earlier and plug in Fα(u) in place of F(u):
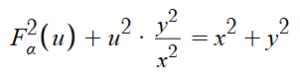
This equation can then be turned into a differential equation by plugging in y = 1, isolating Fα(u), and taking the derivative of both sides with respect to u. x is a function of u, so this equation can be solved for du/dx in terms of x, u, and α. By graphing the slope field and approximate solution curve to this equation, we can visualize the transformation of the Euclidean line y = 1 into the Non-Euclidean transformation of this line in our example surface.
This was the first thing that I got done this week, and I will link a graph of it at the end of this post. However, something more important that I began exploring was perhaps the most useful application of pseudoconics that I have yet come up with: using pseudoconics to analyze Non-Euclidean geometries. Imagine that you have a certain, known Non-Euclidean geometry which warps some Euclidean function y = f(x) into some Non-Euclidean curve (u, g(u)). Then, take the pseudoparabola of f(x) in the Euclidean plane, and graph this pseudoparabola using geodesic projections onto the Non-Euclidean surface. After that, use geodesic lines to find the shortest 3-dimensional distance between a point (u, g(u)) on the surface and its corresponding point on the Non-Euclidean pseudoparabola on the surface. Find the parametric projection of this geodesic line, and find its arc length, and what you have just found is the metric which describes that Non-Euclidean geometry. For those who are unaware, metrics in the context of Non-Euclidean geometries are defined as the shortest distance between any two points in that geometry. For instance, the metric of Euclidean geometry is simply the Pythagorean distance between two points. Recall that pseudoparabolas are defined as the shortest equal distance between a focus point and a directrix curve, so the distance between a point on a curve and the corresponding point on its pseudoparabola must be the shortest distance between those two points. I have not finished exploring this idea yet, but if it proves successful, then it may be possible to use pseudoconics to find metrics for any Non-Euclidean geometry, which would be a massively groundbreaking application for pseudoconics, and a great way to end the 10 weeks of my Senior Project. For now, I will link some more graphs down below, but I look forward to sharing the final week of my project with you all next week!
Non-Euclidean Transformation: https://www.desmos.com/calculator/yurgt3lxcq
Non-Euclidean Transformation 3D: https://www.desmos.com/3d/we92fkfkhe
