#3 – More Pseudoconics
Paul N -
Welcome to week 3 of my Senior Project! At this point, we have begun to completely deviate from the original plan for our Senior Project and instead have been putting tons of effort into studying pseudoconic curves and learning more about them. There is so much new mathematics to be discovered with these curves! First off, I should say that ‘pseudoconic’ may be a misleading word to describe the curves we have seen so far; a better term would be ‘pseudoparabola’ since the curves that we have studied so far have been based on the directrix-focus definition of a parabola. Next week, we are looking forward to studying pseudoellipses and pseudohyperbolas, but this week, our focus was on 3 things: expanding pseudoparabolas into 3 dimensions, mapping 2-dimensional pseudoparabolas onto a sphere (which we began working on last week), and expanding 2-dimensional pseudoparabolas to non-linear parametric directrix curves. So, a whole lot has happened this week, and I will try my best to give a brief but holistic overview of each of them.
First off, in order to expand pseudoparabolas into 3 dimensions, the process is similar for two dimensions: take a focus point (h,k,l) and a non-linear directrix curve, d(x,y). Then, take a test point (u0, v0, d(u0,v0)) on the directrix curve and find the equation of the plane tangent to the curve at this point:

For those who are unfamiliar with partial derivatives, a partial derivative involves taking the derivative of a multivariable function with respect to only one variable, treating all other variables as constants (for example, the partial derivative of f(x,y) = x^2 + y^2 with respect to x is 2x). Then, we can find two other points on the tangent plane, and take the cross product of these two points to find the equation of a line perpendicular to the tangent plane which passes through our original test point. For those unfamiliar with cross products, I won’t go into the details here, but many are probably familiar with dot products from physics class, which are very similar to cross products. The equation of a line in 3 dimensions can be written as 3 parametric equations of one variable t, and so if we take the following to be our two points on the tangent plane, the resulting parametric equation is:
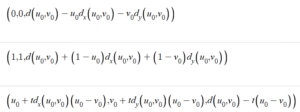
Then, find the midpoint between the focus point and the test point, and find the parametric equation of the line connecting the test point to this midpoint. This will also be the line connecting the test point to the focus.
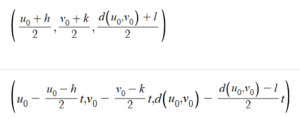
Next, find the equation of the plane perpendicular to this line and that passes through the midpoint. The slope of the x, y, and z coordinates of the plane will be equivalent to the slopes of t in the x, y, and z parametric equations of the line that it is perpendicular to, so:
Now, just like we did last week for 2-dimensional pseudoparabolas, we have an isosceles triangle whose two congruent sides are equal to the distance from a point on the pseudoparabolic curve to the focus and to the test point. Now, all we have to do is find the intersection between the plane which we just derived and the line which was perpendicular to the directrix curve at the test point, and we can do this by plugging in each of the 3 parametric equations from the line equation as x, y, and z in the plane equation, and after much algebra, we can solve for a value of t, t0, in terms of u0 and v0. Then, we can plug this value of t back into the line equation to get the x, y, and z coordinate of the intersection of the plane and the line. By generalizing u0 and v0 to be any values u and v, we have obtained the full parametric surface (in 3 dimensions, parametric equations of two variables u and v create a parametric surface, as opposed to a parametric curve which is simply a line). The equation is too long to list out here, but I will link the Desmos 3D graph at the bottom of this post for those who wish to view it.
That was the vast majority of the math in this post. It turns out that the second goal of mapping 2-dimensional pseudoparabolas onto a sphere is rather simple: take a sphere of radius α which is above the xy-plane in 3 dimensions, and imagine that on the xy-plane our pseudoparabolic curve is drawn out. Take any point (x(t0), y(t0)) on the curve and create a line in 3 dimensions connecting this point to the point at the top of the sphere. Find the intersection of this line with the sphere that isn’t the top of the sphere, and generalize this equation to fully map a portion of the pseudoparabolic curve onto the sphere, and then change the z-coordinate of the resulting 3-dimensional curve to map it onto our original sphere which was centered at the origin and facing upwards. I will avoid boring you with more math, but the result is fascinating:
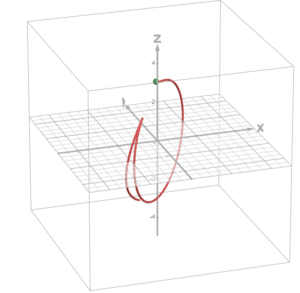
Just as we predicted in my last post! Here, we have the pseudoparabolic curve from my last post wrapped around a sphere of radius 3, restricted on the domain 0<t<3, and we can clearly see that it is, in fact, “wrapping” itself around the sphere as it approaches infinity in the first quadrant and extends upwards from negative infinity in the third quadrant.
Finally, our third goal this week, finding 2-dimensional pseudoparabolas for parametric directrix curves, was even simpler: all we had to do was slightly revise our original equations to account for the x(t) component of the directrix, as well as changing the derivative d'(t) to be y'(t)/x'(t) since d'(t) = dy/dx = (dy/dt)/(dx/dt). Take a look at the pseudoparabolas that occur when our parametric directrix curve is a circle and we move the focus horizontally along the x-axis:
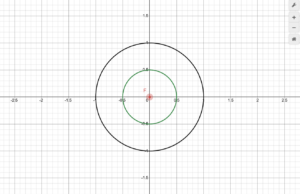
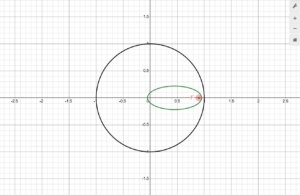
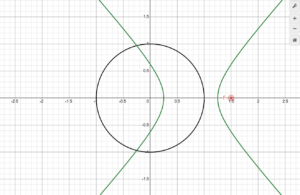
Now we have obtained the familiar conic sections! It turns out that this relation of conic sections to circles has been known for thousands of years, though I didn’t know about it until a few days ago. Either way, there are some fascinating curves to be seen with all 3 of the graphs that I have made here, so I will link them all below for anyone who would like to try them (the third graph is highly unpolished, since this is where I began working on deriving pseudoellipses and pseudohyperbolas, though I was not able to finish last week):
https://www.desmos.com/3d/dxsjfh5adn
https://www.desmos.com/3d/5h0zk29xd0
https://www.desmos.com/calculator/ewyg57j05g

Comments:
All viewpoints are welcome but profane, threatening, disrespectful, or harassing comments will not be tolerated and are subject to moderation up to, and including, full deletion.