#10 – Metrics and Non-Euclidean Derivatives
Paul N -
Hi, and welcome to the final week of my Senior Project. My original goal for this week was to find a way to use pseudoconics to analyze Non-Euclidean geometries via metrics, and while this did not end up happening, I ended up finding an arguably much more interesting application for pseudoconics within Non-Euclidean geometry. Firstly, I will discuss how to develop metrics for Non-Euclidean geometries, and it turns out that this process is rather simple. The first step is to take any two points in the Non-Euclidean geometry (u0, v0) and (u1, v1) and find the geodesic line between these two points plotted on the 3-dimensional Non-Euclidean surface. The 3-dimensional geodesic line connecting these lines will form a parametric equation of the form (u, v, z(u,v)), where v as a function of u is defined to be the following (recalled from a previous post):
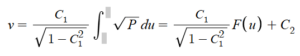
We can solve for C1 and C2 using a system of equations for the two points on this line (u0, v0) and (u1, v1), and we get the following:
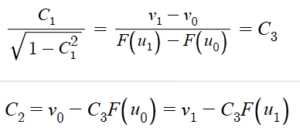
From here, v(u) = C3F(u) + C2. Since metrics are two-dimensional, we can discard the z-coordinate in our parametric equation (u, v, z(u,v)), and now all we are left with is the line (u, v(u)) from the point (u0, v0) to (u1, v1). We can now apply the arc length formula to obtain a formula for the metric of our Non-Euclidean geometry:
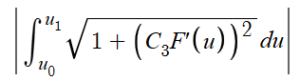
Note that this formula makes sense: in the ordinary Euclidean geometry, F(u) = u, and solving this integral with this F(u) yields the Euclidean metric (the Pythagorean distance formula). The absolute value bars around the integral are necessary because metrics are defined to be positive, and in the case where u0 > u1, the metric would be negative without these absolute value bars.
The next topic, and the main highlight of this week, is applying pseudoconics to discover a special kind of Non-Euclidean derivative. While it turns out that Non-Euclidean derivatives are an existing subject, the kind of derivative that we have found here is different from a conventional derivative, and while it does yield a numerical value, the concept is much more meaningful than the numerical value. Recall from one of my very first posts that one of the steps involved in finding a pseudoparabola is finding the line perpendicular to the directrix curve at a point (t, d(t)). If both the directrix curve and pseudoparabola are transformed into a certain Non-Euclidean geometry, we end up with a strange situation where there are sort of two different perpendicular lines to the resultant directrix at the correspondent point to the Euclidean point (t, d(t)) on the directrix. It turns out that transforming the perpendicular line from the Euclidean plane into the Non-Euclidean geometry results in a false perpendicular line in the Non-Euclidean geometry, which intersects the correspondent point on the directrix but neither intersects the resultant pseudoparabola nor is actually perpendicular to the resultant directrix. On the other hand, there is a true perpendicular line which can be found by finding the geodesic line connecting the correspondent point on the directrix to the correspondent point on the pseudoparabola, though again it turns out that this line is not actually conventionally perpendicular to the resultant directrix. This is to be expected, though, since perpendicularity is different in Non-Euclidean geometries, and we can say that this is the true perpendicular because of its connection to the pseudoparabola.
The equation of the true perpendicular in two dimensions is (u, v(u)), which is similar to the equation we just used to solve for Non-Euclidean metrics, only this time the two points being connected are different. If we have the Non-Euclidean curve v = f(u), which is the Non-Euclidean transformation of some Euclidean curve y = d(x), and we want to find its Non-Euclidean derivative at the point (u0, v0), then the following familiar equation will need to be used to find the points (u0, v0) and (u1, v1) in the Non-Euclidean geometry which correspond to the points (t, d(t)) and (x0(t), y0(t)) in the Euclidean plane which are the directrix and pseudoparabola points, respectively (remember that v = u*y/x):

Once the true perpendicular is found, take its conventional derivative with respect to u at u = u0, and find the negative reciprocal of the derivative to find the Non-Euclidean derivative of v = f(u) at u = u0. As I mentioned before, while this process does yield a numerical value, the conceptual value is of much more importance; in this case, the conceptual value is that this gives us a sort of comparison of the rate of change of a curve in the Non-Euclidean geometry to its rate of change in the Euclidean plane. For example, take the line y = x, and assume that F(u) in our Non-Euclidean geometry is the square root of u cubed. It turns out that the line y = x is transformed into the line v = u, and the Non-Euclidean derivative of v = u is slightly less than 1 for small values of u, and much less than one but greater than zero as u increases. This is what our Non-Euclidean geometry looks like in 3 dimensions:
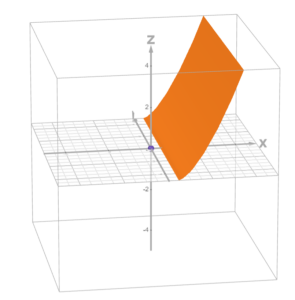
In this context, our Non-Euclidean derivative makes sense: when u is small, the Non-Euclidean surface approaches a normal Euclidean plane, so the derivative of v = u approaches the derivative of y = x, and when u is large, the Non-Euclidean surface begins to slope intensely in the z-direction, slowing its rate of change in the u-v plane. Interestingly enough, it turns out that there is also a chain rule for Non-Euclidean derivatives:

So it is very similar to normal chain rule, except the chain derivative is inverted. There is another kind of Non-Euclidean derivative that we can look at, which is the one that arises when looking at the false perpendicular. If we have a function uE(x) which represents the u-coordinate on the false perpendicular corresponding to an x-coordinate on the Euclidean perpendicular, and then we have the line y = yp which is the perpendicular line to the directrix at (t, d(t)), then the equation of our false perpendicular will be (uE(x), uE(x)*yp/x). Then, we can take the derivative of this parametric function with respect to x at the point (u0, f(u0)) and find its negative reciprocal to find the alternate Non-Euclidean derivative:
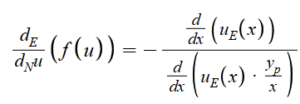
We would expect the chain rule for this alternate derivative to be the following:
However, upon calculating numerical values, it appeared that the numbers did not match up for this to be the proper chain rule, though I ran out of time to discover why that would be the case. I’m also unsure as to what the conceptual significance of this alternate derivative would be, though I would imagine it to be some kind of inverse to the true Non-Euclidean derivative since it is formed from the false, Euclidean perpendicular rather than the true, Non-Euclidean perpendicular. Either way, this concludes my Senior Project. Once again, I will link some graphs at the end of the post, but I would like to thank you all for accompanying me on this journey. I believe that this is just the beginning of my research on pseudoconics and many other topics that I’ve explored here, and I will likely continue this research throughout the summer and during my time in college. I hope to anyone reading this that you have found interest in and enjoyed reading my blog posts!
Metric for F(u) = sqrt(u^3) at y = 1 and pseudoparabola for y = 1: https://www.desmos.com/calculator/hsbuqktg5n
General metric for F(u) = sqrt(u^3): https://www.desmos.com/calculator/ivfty06ic6
Non-Euclidean derivative: https://www.desmos.com/calculator/peecezukrq
Non-Euclidean derivative (chain rule): https://www.desmos.com/calculator/2xmtdkttmb
