Week 6: Houston, we have a problem…

Kira A -

Welcome back, everyone! I hope you are all having (or probably had by the time you are reading this) a great spring break. This past week I have been focusing on different approaches to establishing a Translunar Injection Orbit (TIO) from an initial Low Earth Orbit (LEO). This photo is of the first method I came up with for the orbit-raising maneuver using the modified rocket equation I have previously spoken about. It makes use of the delta-v value that can be found using the rocket equation and combines that delta-v value with the previous velocity of the spacecraft at the perigee point.

 

After coding it into MATLAB and comparing it with a traditional single burn transfer orbit, I found that it did not produce the desired results. It uses the same amount of fuel to create the same effect as a singular burn, so I need to figure out a different approach to the orbit-raising maneuver if I am to create a more efficient trajectory to the Moon.

 

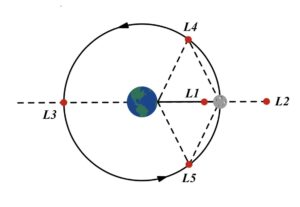
Beyond the trajectory/transfer orbit to the Moon, I am also considering different types of orbits around the Moon (selenocentric orbits) once my spacecraft arrives. One of the orbit families I am considering is the halo orbit family. This family features highly eccentric orbits that are associated with one of the Earth-Moon Lagrange points. Lagrange, or libration, points are areas of space where a small object experiences equal influence from the gravitational forces of two more massive objects, in this case, the Earth and the Moon. The halo orbit family is of particular interest for my mission because the NASA Lunar Gateway mission plans to make use of a near-rectilinear halo orbit (NRHO), meaning that if my spacecraft is to dock with the Gateway station, it must be inserted into this orbit as well. The NRHO, due to its orientation in space around the Moon, allows the spacecraft to always have a direct line of sight with the Earth; thereby enabling an open line of communication between the spacecraft and ground control at all times. I will be exploring the different options in the coming weeks as we get deeper into the mission!

Earth-Moon Lagrange points 1-5

 

This week I plan to continue my work on the orbit-raising maneuver at the Arizona State University – Tempe campus, as I will have access to some of the resources there this Thursday to help maximize my efforts. I am also considering bolstering the spacecraft design element of my mission, however, I need to run this by my mentors Mr. Joseph, Dr. Farooq, and Dr. Goodwin for their approval. 

 

Thank you again to my mentors for giving their time and thought to this project and guiding me as I navigate each challenge throughout. Thank you all for tuning back in or joining in if it’s your first time! I hope to bring you some more exciting findings next time. 

 

Ad Lunam!




More Posts

Comments:

All viewpoints are welcome but profane, threatening, disrespectful, or harassing comments will not be tolerated and are subject to moderation up to, and including, full deletion.

    mihika_g
    Your updates are always so intriguing, Kira! Could you clarify a little more on the Lagrange points and their utility in the selenocentric orbits?
    March 24, 2025 at 10:48 am - Reply
    camille_bennett
    Hi Kira, so great that you will have access to some ASU resources. Do you have any ideas as to why your orbit raising maneuver did not produce your anticipated results?
    March 25, 2025 at 8:38 am - Reply
    kira_a
    Great question, Mihika! Earth-Moon Lagrange points are useful in selenocentric orbits because their unique gravitational properties allow a spacecraft to maintain an orbit around the Moon with little to no stationkeeping, or fuel used to stay in orbit. I hope this helps :)
    March 27, 2025 at 11:16 am - Reply
    aashi_h
    Hi Kira, your project is so fascinating! Do you have any idea of what different orbit-raising maneuver you might turn to next for your space mission?
    March 27, 2025 at 11:19 am - Reply
    kira_a
    Hi Mrs. Bennett, I believe that the method of orbit raising I talked about in this blog did not produce the outcome I wanted because it did not consider the total energy of the spacecraft in its orbit. This method only considers the spacecraft's velocity, which corresponds to the kinetic energy, however, gravitational potential energy is also a part of the spacecraft's total energy. So, I need to find a method that takes into account both kinetic and gravitational potential energy, which I use in my most recent blog. Thank you for the good question!
    March 27, 2025 at 11:20 am - Reply
    kira_a
    Hi Aashi, thank you so much! I touched upon it in my most recent blog, but the method of orbit raising that I am planning to pursue further uses burns at both perigee and apogee points as opposed to only perigee burns like the one I discuss here. This allows me to raise the energy of the orbit, and approach the energy required to reach the Moon, with less fuel expended. The reason I believe this will be the best option for my mission is because it has already been used in real-world applications during the Chandrayaan 3 mission carried out by ISRO.
    March 27, 2025 at 11:27 am - Reply
    Akash Joseph
    Hi Kira, Great work on the analysis! I love your figure depicting the Lagrange points for the Earth-Moon system. How are you drawing these figures and would all of these be included in your final report?
    March 27, 2025 at 11:41 am - Reply
    kira_a
    Hi, Mr. Joseph! I have been using the Goodnotes application to design the figures I have included in my blogs and will also include them in my final report.
    April 11, 2025 at 12:31 pm - Reply

Leave a Reply

Your email address will not be published. Required fields are marked *