Week 3: Basic Bayesian Inference: Evaluating Hitter Performance
Ian M -
This week, I’ve continued my exploration of Bayesian statistics in baseball, and my focus this week was on evaluating hitter performance, particularly looking at how batters perceive pitching and adjust to information while hitting. The first part of my work focused on posterior probability, specifically in relation to individual batters and their responses to observed pitching performance.
In Bayesian statistics, posterior probability is a way of updating our beliefs about a batter’s ability based on new data. Instead of just observing their batting average, Bayesian methods allow us to account for how a batter perceives and reacts to the information they gather while facing pitchers. Every time a batter steps up to the plate, they are gathering information such as pitch types, pitch locations, and pitcher tendencies which they use to adjust their hitting strategy. By analyzing these adjustments, we can model the batter’s response to different types of pitches over time.
This process works by taking into account prior knowledge of the batter’s skill level—perhaps their performance in previous seasons or against similar pitchers—and updating that belief with each new observation. For example, if a batter starts the season struggling against fastballs but adjusts their swing mechanics after a few games, Bayesian inference helps us update our understanding of their hitting ability. We can calculate the posterior probability of the batter’s true ability to hit fastballs, accounting for both their previous performance and the new data from the most recent games. Over time, this helps us form a more accurate picture of how a batter is adjusting and whether they are improving or regressing in response to different types of pitchers.

Part B is a breakdown of each aspect of a pitcher’s delivery and the pitch itself and their influence on how batters perform against those pitches.
Part C shows how ball position is estimated by batters by accounting for prior belief and observed factors simultaneously to form a posterior distribution.
Part D displays that relying on posterior distributions rather than prior or observed data only creates the best likelihood of successful batting.
Image credit to Bayesball: Bayesian Integration in Professional Baseball Batters by Justin A. Brantley and Konrad P. Körding.
The second part of my work this week centered on the streakiness of hitters and their odds of slumping. Baseball is known for its streaky nature, with players sometimes experiencing hot streaks followed by cold spells. Traditionally, these streaks are just seen as random fluctuations in a player’s performance. However, Bayesian methods allow us to directly quantify the likelihood of a slump occurring based on a player’s previous performance and the variability inherent in the game.
By using Bayesian models to analyze the fluctuations in a batter’s performance, we can estimate the probability of a hitter entering a slump, given their recent history. For instance, if a batter has been consistently performing above their career average, Bayesian inference allows us to predict the probability of them regressing to the mean. Conversely, if a player is struggling, Bayesian models can help us calculate the likelihood of them recovering and returning to their usual performance levels. The power of this approach is that it provides a more nuanced understanding of these streaks, allowing us to model not only the player’s talent but also the uncertainty and variability that are inherent in baseball.
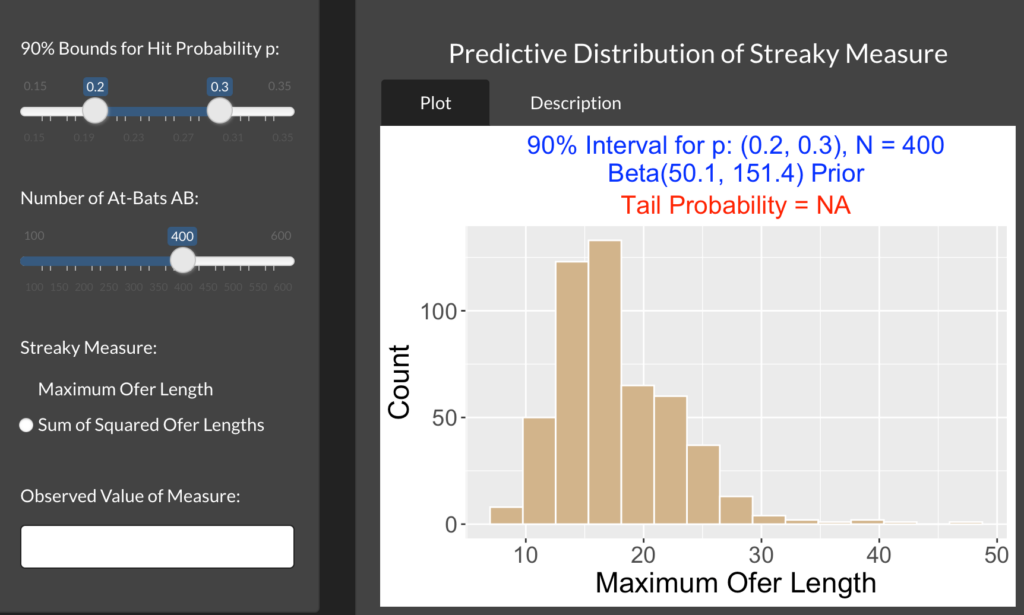
Ultimately, this week’s exploration of Bayesian statistics has helped me develop a deeper understanding of how hitters adjust to pitching and how their performance can fluctuate over time. By modeling how batters update their beliefs based on pitch selection and how likely they are to experience slumps, we can provide more sophisticated predictions of their future performance. This week’s work has reinforced the value of Bayesian methods in capturing the complexities of baseball, and how they allow us to view player performance through a probabilistic lens, improving our ability to make informed assessments.

Comments:
All viewpoints are welcome but profane, threatening, disrespectful, or harassing comments will not be tolerated and are subject to moderation up to, and including, full deletion.